Archivos suplementarios
Cómo citar
Descargas
Métricas Alternativas
Dimensions
Resumen
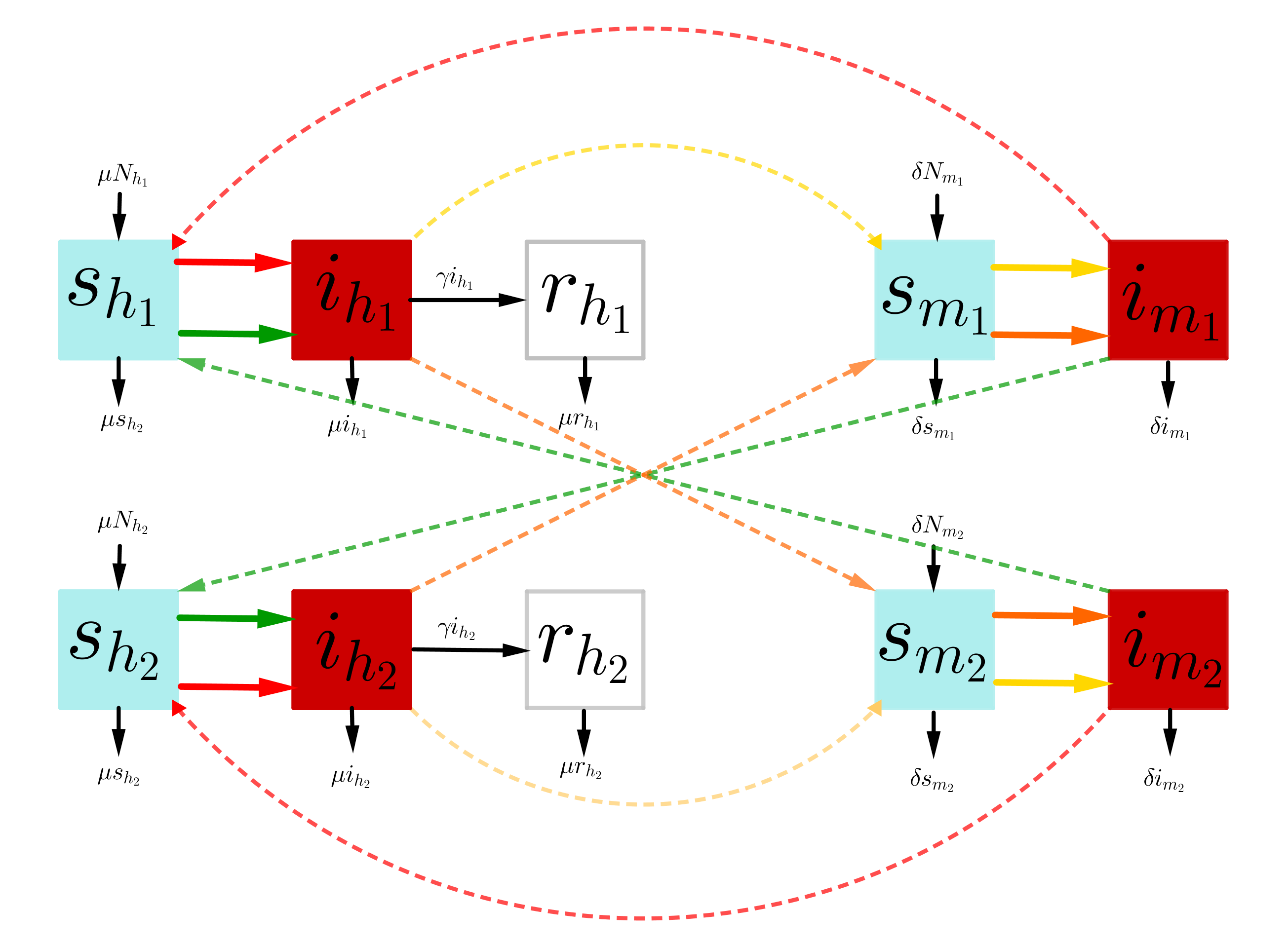
No es una novedad que el crecimiento de las poblaciones urbanas está aumentando, especialmente en zonas de bajos recursos. Dicho crecimiento viene acompañado de servicios de saneamiento ambiental deficientes y falta de recursos para el almacenamiento adecuado del agua, lo que ha favorecido el crecimiento de la población de mosquitos y, por ende, la propagación del dengue. El dengue es una enfermedad viral transmitida principalmente por los mosquitos Aedes aegypti que constituye uno de los mayores problemas de salud pública. El análisis cualitativo y cuantitativo de la propagación de esta enfermedad es de suma importancia para la sociedad, pues permite plantear un plan de choque para la prevención de una epidemia. Presentamos el análisis de un modelo metapoblacional del tipo SIR-SI que representa la dinámica del dengue para dos zonas conectadas por los tiempos de permanencia de la población humana en ellas, así como el análisis cualitativo del modelo, considerando diferentes escenarios de conexión entre las dos zonas estudiadas.
Palabras clave
Citas
Arias, J., Martínez, H., Vasilieva, O. (2020). Biological and Chemical Control of Mosquito Population by Optimal Control Approach, Games, 11(4), 62.
Barrios, E., Lee, S., Vasilieva, O. (2018). Assessing the effects of daily commuting in two-patch dengue dynamics: A case study of Cali, Colombia. Journal of Theoretical Biology, 453, 14-39.
Castillo, C. & Brauer, F. (2001). Mathematical models in population biology and epidemiology, Volumen 40, Springer-Verlag, 2001. p. 411-425.
Chitnis, N., Hyman, JM., Cushing, J.M. (2008). Determining important para- meters in the spread of malaria through the sensitivity analysis of a mathematical model. Bulletin of mathematical biology, 70(5), 1272-1296.
Iggidr, A., Sallet, G., Souza, M. (2016). On the dynamics of a class of multi- group models for vector-borne diseases. Journal of Mathematical Analysis and Applications, 441(2), 723-743.
Jacquez, J. & Simon, C. (1993). Qualitative Theory of Compartmental Systems. SIAM Review, 35 (1), 43-79.
Lasluisa, D., Barrios, E., Vasilieva, O. (2019). Optimal strategies for dengue prevention and control during daily commuting between two residential areas. Processes, 7(4), 197.
Martcheva, M. (2015). An introduction to mathematical epidemiology (Vol. 61, pp. 9-31). New York: Springer.
MinSalud (2017), Plan nacional integral e interprogramático para la prevención, el control y la eliminación de las enfermedades infecciosas desatendidas 2013-2017. https://www.minsalud.gov.co/sites/rid/Lists/BibliotecaDigital/RIDE/VS/PP/ET/2013%2007%20Plan%20Interprogram%C3%A1tico%20EID.pdf
Padilla, J., Rojas, D., Saénz, R. (2012). Dengue en Colombia: Epidemiología de la reemergencia a la hiperendemia. Ministerio de Salud. p. 1-13.
Sepúlveda, L. (2015). Manejo óptimo y viable en modelos epidemiológicos de dengue. PhD tesis, Universie´ Paris-Est.
Smith, H. (1995). Monotone Dynamical Systems: an introduction to the theory of competitive and cooperative system, 41, American Mathematical Soc.
Travi, B. & Montoya, J. (1994). Manual de entomología médica para investigadores de América Latina, fundación CIDEIM.
Van den Driessche, P. & Watmough, J. (2002). Reproduction numbers and sub- threshold endemic equilibria for compartmental models of disease transmission. Mathematical biosciences, 180 (1), 29-48.
Velandia, M. L. & Castellanos, J. E. (2011). Virus del dengue: estructura y ciclo viral. Infectio, 15 (1), 33-43.
Esta obra está bajo una licencia internacional Creative Commons Atribución-NoComercial-SinDerivadas 4.0.
Derechos de autor 2022 Revista de la Academia Colombiana de Ciencias Exactas, Físicas y Naturales