Resumen
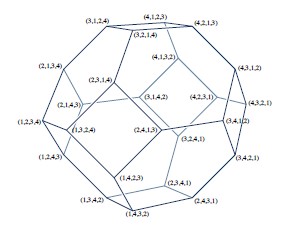
La teoría de Ehrhart mide un politopo P discretamente, contando los puntos enteros dentro de sus dilataciones P, 2P, 3P, ..... En este artículo calculamos la teoría de Ehrhart de cuatro familias de politopos de gran importancia en varias áreas de la matemática: los permutaedros de Coxeter de los grupos clásicos de Coxeter An, Bn, Cn, Dn. Una herramienta central, de interés independiente, es la descripción de la teoría de Ehrhart de una traslación racional de una proyección entera de un cubo.
Referencias
Ardila, F., Castillo, F., Eur, C., & Postnikov, A. (2020). Coxeter submodular functions and deformations of Coxeter permutahedra. Adv. Math. 365: 107039.
Ardila, F., Castillo, F., & Henley, M. (2015). The arithmetic Tutte polynomials of the classical root systems. International Mathematics Research Notices. 2015 (12): 3830-3877.
Ardila, F., Supina, M., & Vindas-Meléndez, A. R. (To appear). The equivariant Ehrhart theory of the permutahedron. Proceedings of the American Mathematical Society. (arXiv:1911.11159)
Bárány, I., & F¨uredi, Z. (1987). Computing the volume is difficult. Discrete & Computational Geometry. 2 (4): 319-326.
Beck, M., & Robins, S. (2015). Computing the Continuous Discretely: Integer-point Enumeration in Polyhedra (Second ed.). Springer, New York. Retrieved from http://dx.doi.org/10.1007/978-1-4939-2969-6 (electronically available at http://math.sfsu.edu/beck/ccd.html) doi:10.1007/978-1-4939-2969-6
Coxeter, H. S. M. (1973). Regular Polytopes. Courier Corporation.
De Concini, C., & Procesi, C. (2008). The zonotope of a root system. Transform. Groups. 13 (3-4):507-526.
Deza, A., Manoussakis, G., & Onn, S. (2018). Primitive zonotopes. Discrete Comput. Geom. 60 (1): 27-39.
Dyer, M. E., & Frieze, A. M. (1988). On the complexity of computing the volume of a polyhedron. SIAM Journal on Computing. 17 (5): 967-974.
Ehrhart, E. (1962). Sur les polyèdres rationnels homothétiques à n dimensions. C. R. Acad. Sci. Paris. 254: 616-618.
Fukuda, K. (2008). Software package cdd. (Electronically available at http://www.ifor.math.ethz.ch/fukuda/)
Humphreys, J. E. (1978). Introduction to Lie Algebras and Representation Theory (Vol. 9). Springer-Verlag, New York-Berlin. (Second printing, revised)
Humphreys, J. E. (1990). Reflection Groups and Coxeter Groups (Vol. 29). Cambridge University Press, Cambridge. Retrieved from https://doi.org/10.1017/CBO9780511623646 doi: 10.1017/CBO9780511623646
McWhirter, J. (2019). Ehrhart quasipolynomials of Coxeter permutahedra (Master’s thesis, San Francisco State University). https://sfsu-space.calstate.edu/bitstream/handle/10211.3/213961/AS362019MATHM39.pdf?sequence=1.
Shephard, G. C. (1974). Combinatorial properties of associated zonotopes. Canad. J. Math. 26 (2):302-321.
Sloane, N. (n.d.). The On-Line Encyclopedia of Integer Sequences. (published electronically at http://oeis.org, 2014)
Stanley, R. P. (1991). A zonotope associated with graphical degree sequences. In Applied geometry and discrete mathematics (Vol. 4, pp. 555-570). Providence, RI: Amer. Math. Soc.
Stanley, R. P. (1999). Enumerative Combinatorics. Volume 2 (Vol. 62). Cambridge: Cambridge University Press. (With a foreword by Gian–Carlo Rota and appendix 1 by Sergey Fomin)
Stapledon, A. (2011). Equivariant Ehrhart theory. Advances in Mathematics. 226 (4): 3622-3654.
Zaslavsky, T. (1981). The geometry of root systems and signed graphs. Amer. Math. Monthly. 88(2): 88-105.
Zaslavsky, T. (1982). Signed graphs. Discrete Appl. Math. 4 (1): 47-74.
Zaslavsky, T. (1998). A mathematical bibliography of signed and gain graphs and allied areas. Electron. J. Combin. 5. Dynamic Surveys 8, 124 pp. (Electronically available at http://www.math.binghamton.edu/zaslav/Bsg/index.html)

Esta obra está bajo una licencia internacional Creative Commons Atribución-NoComercial-SinDerivadas 4.0.
Derechos de autor 2020 Revista de la Academia Colombiana de Ciencias Exactas, Físicas y Naturales